高校1年の図形と計量で学習します、「余弦定理」を紹介します。
余弦定理とは
余弦とはコサイン(cos)を表してまして、コサインが式の中に登場します。直角三角形じゃないと使えないとか、二等辺三角形じゃないと使えないというわけでなく、すべての三角形に使えます。
三角形の何について?
すべての三角形に使えるとお伝えしましたが、三角形の何について使うかといいますと、三角形の角の大きさと辺の長さについて使います。三角形には3本の辺と、3つの角(内角)がありますがそのうちの3本の辺の長さと、1つの内角を使います。4つのうちどれかひとつは分からないので文字でおくことになります。(問題によっては2つ以上がわからないこともありますが。)
余弦定理の紹介(定理によって成り立つ等式の紹介)
教科書・参考書・問題集を御覧頂きますと、余弦定理の式は3つ、次のようにあります。
三角形ABCについて
$$a^2 =b^2 +c^2 -2bc\cos A$$
$$b^2 =c^2 +a^2 -2ca \cos B$$
$$c^2=a^2 +b^2 -2ab \cos C$$
(ここで小文字a,b,cは角A,B,Cの向かい側の辺の長さで三角形ABC特有の呼び方です。)
3つもあって、さらに変形した等式が載っている場合もあります。
もちろん、正しく覚えるのならばすべて覚えていただいてもよいでしょうが、まずは次のように1種類覚えていただくのがよろしいかと存じます。
式の立て方のポイント 位置関係が重要
まずは、正しく等式を立てることが大事です。ポイントとしましては
三角形の位置関係に特に注意して立てると良いでしょう。
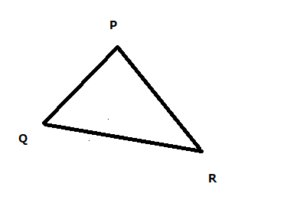
①まずひとつの辺に注目する。
たとえば、上の三角形のPRに注目することにしましょう。
②注目した辺の向かい合う角とのこりの2辺に着目する。
辺PRの向かい合う角は角Qでのこりの2辺はPQとQRですね。
③等式をたてる
「身につけ方」
やはり実際に使ってみることで身についていきます。
最初は教科書の式を見ながらでも(解き方を先に見てしまっても)構いませんので、
シンプルな問題を解いて使い慣れていってください。
問題例
三角形ABCにおいて、∠A=60°、辺ABの長さは2(つまり小文字c=2),辺CAの長さは3(つまり小文字b=3)
であるとき、辺BCの長さを求めましょう。

実際に式を立ててみましょう。
余弦定理を使ってみます。
注目する辺は?
さきほど注目する辺といいましたが、どこに注目するか説明してなかったのですが、余弦定理は3本の辺(の長さと)ひとつの内角が登場する定理です。
したがって、使う角の向かい側が注目する辺(左辺におくもの)ということができます。
今ですと、角Aの向かい側が辺BCなので
BCの2乗イコール・・・という式をたてます。辺BCは頂点Aの向かい側ですので辺BCの長さをaと表します。
余弦定理より
$$a^2 =2^2 +3^2 -2\times 2\times 3 \times \cos 60^{\circ}$$
右辺の計算をすすめます。
(cos60°は2分の1ですから)
$$a^2=4+9-2\times 2 \times 3 \times \frac{1}{2} =13-6=7$$
となり
$$a>0よりa=\sqrt{7}すなわちBC=\sqrt{7}$$
となります。



コメント